Capteur résistif - CTN (seconde générale)
Principe
La résistance électrique d’un capteur résistif varie en fonction de la grandeur physique mesurée (ex. température, pression, intensité lumineuse, …).

Capteur de température CTN / Capteur de lumière LDR
Pour obtenir une valeur de cette grandeur physique, il est nécessaire de mesurer la résistance du capteur.
Malheureusement un microcontrôleur ne mesure que des tensions sur ses entrées analogique (ex. A0, A1, … pour Arduino). Il faut donc adapter le capteur dans un montage électrique (ex. pont diviseur de tension, pont wheatstone).
Montages pour la mesure d’une résistance
La plupart des modules avec capteur résistif utilise un pont diviseur de tension pour la mesure de la résistance du capteur. Par rapport au pont Wheatstone, cette méthode présente l’avantage d’être simple à mettre en oeuvre.
Montage 1 : capteur connecté à la masse
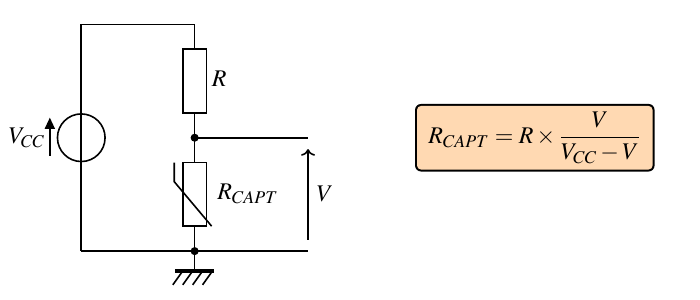
VCC est la tension d’alimentation du microcontrôleur.
L’entrée analogique A0 mesure la tension \(V\) aux bornes du capteur résistif.

Module Velleman VMA320 (\(R_1=10\rm~k\Omega\))
Montage 2 : capteur connecté à Vcc
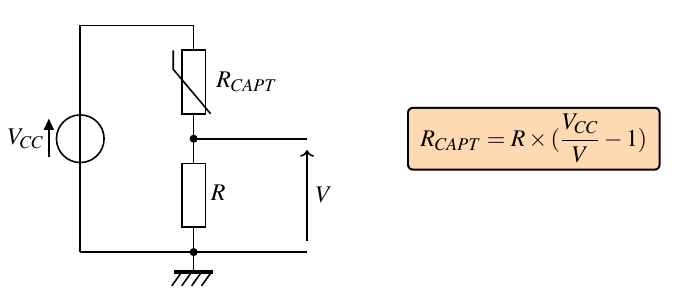
VCC est la tension d’alimentation du microcontrôleur.
L’entrée analogique A0 mesure la tension \(V\) aux bornes de la résistance \(R\).

Module Grove - Temperature Sensor V1.2 (\(R_1=100\rm~k\Omega\))

Module CTN Plug’uino (\(R_1=10\rm~k\Omega\))
Montage 3 : mesure de la tension et du courant (ex. capteurs Educaduino)
En plus de la mesure de la tension du capteur, une mesure du courant est aussi réalisée à partir de la tension aux bornes de la résistance R par l’intermédiaire d’un amplificateur différentiel. La résistance du capteur est alors calculée avec la loi d’Ohm.

L’entrée analogique A0 mesure la tension \(V\) aux bornes du capteur résistif.
L’entrée analogique A1 mesure la tension \(V_R\) aux bornes de la résistance \(R\).

Module CTN 10K Educaduino LAB (\(R_1=10\rm~k\Omega\))
Cas d’un capteur résistif CTN
Une CTN est un capteur résistif à coefficient de température négatif …
Courbe d’étalonnage
Les mesures sont effectuées avec un thermomètre et un ohmmètre.
T (°C) |
R (Ohm) |
|---|---|
2.4 |
25455 |
5.1 |
22714 |
10.0 |
18622 |
15.1 |
15201 |
20.0 |
12607 |
25.0 |
10475 |
30.0 |
8740 |
35.1 |
7333 |
40.0 |
6194 |
45.0 |
5217 |
50.0 |
4358 |
55.1 |
3689 |
60.0 |
3120 |
65.1 |
2647 |
70.1 |
2264 |
75.1 |
1926 |
80.0 |
1658 |
Téléchargement : data_ctn_1.txt (mesures au format CSV).
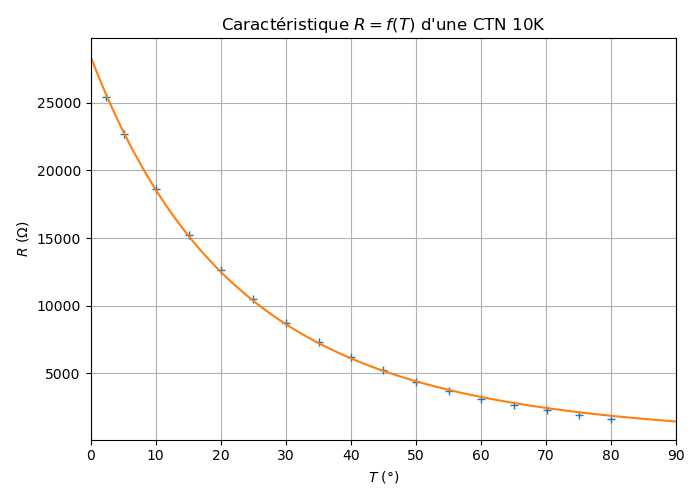
Courbe d’étalonnage d’une CTN 10k
Note
Dans cet exemple, la résistance mesurée prend la valeur particulière de 10 \({\rm k\Omega}\) pour 25°C !
Relation de Steinhart-Hart
Sur une grande plage de variation, la relation entre la température (en K) et la résistance de la CTN est :
A, B et C sont les coefficients de Steinhart-Hart. Ils sont donnés par le constructeur
ou peuvent se déterminer expérimentalement à l’aide du programme Python steinhart-hart.py à partir de trois points de la courbe d’étalonnage.
Résultats obtenus à partir du programme Python :
Relation simplifiée de Steinhart-Hart
Sur une plage de variation plus réduite de la température, la relation de Steinhart-Hart permet d’écrire :
\({R_0}\) est la valeur de la résistance pour la température \({T_0}\).
\({\beta}\) est le coefficient de température (en K).
Ces coefficients sont généralement donnés par le constructeur (datasheet).
Module |
Référence CTN |
\(R_0~{\rm (k\Omega)}\) |
\(\beta~{\rm (K)}\) |
|---|---|---|---|
Grove - Temperature Sensor V1.2 |
NCP18WF104F03RC |
\(100\) |
\(4255~(25/80{\rm^\circ C})\) |
Velleman VMA320 |
NTC-MF52 3950 |
\(10\) |
\(3950\) |
Note
Expression de la constante \(\beta\) à partir des températures \(T_0\) et \(T\) :
Les coefficients \({R_0}\) et \({\beta}\) peuvent être également déterminés par une modélisation de la caractéristique sur la plage de température d’utilisation de la CTN.
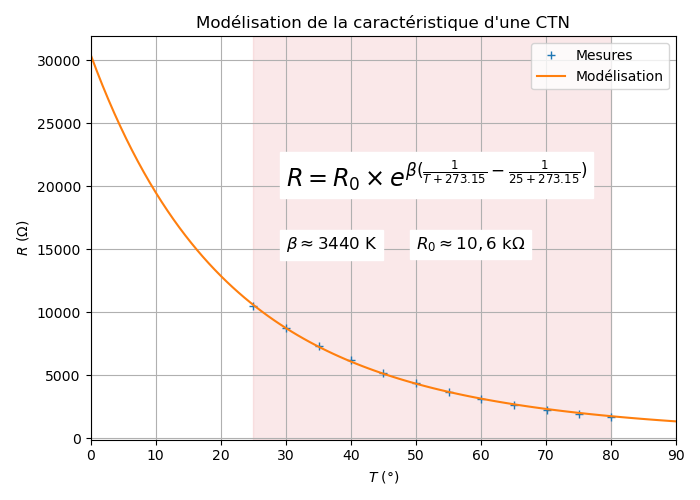
Modélisation de la caractéristique de la CTN de 25°C à 80°C
Résultat de la modélisation de \(T_0 = 25{\rm^\circ C}\) à \(80{\rm^\circ C}\) :
Inversement, le calcul de la température (en K) s’obtient à partir de la relation suivante :
Programme 1 : mesure de la résistance de la CTN
La CTN est connectée à la masse (montage 1). L’entrée analogique A0 mesure la tension du capteur.
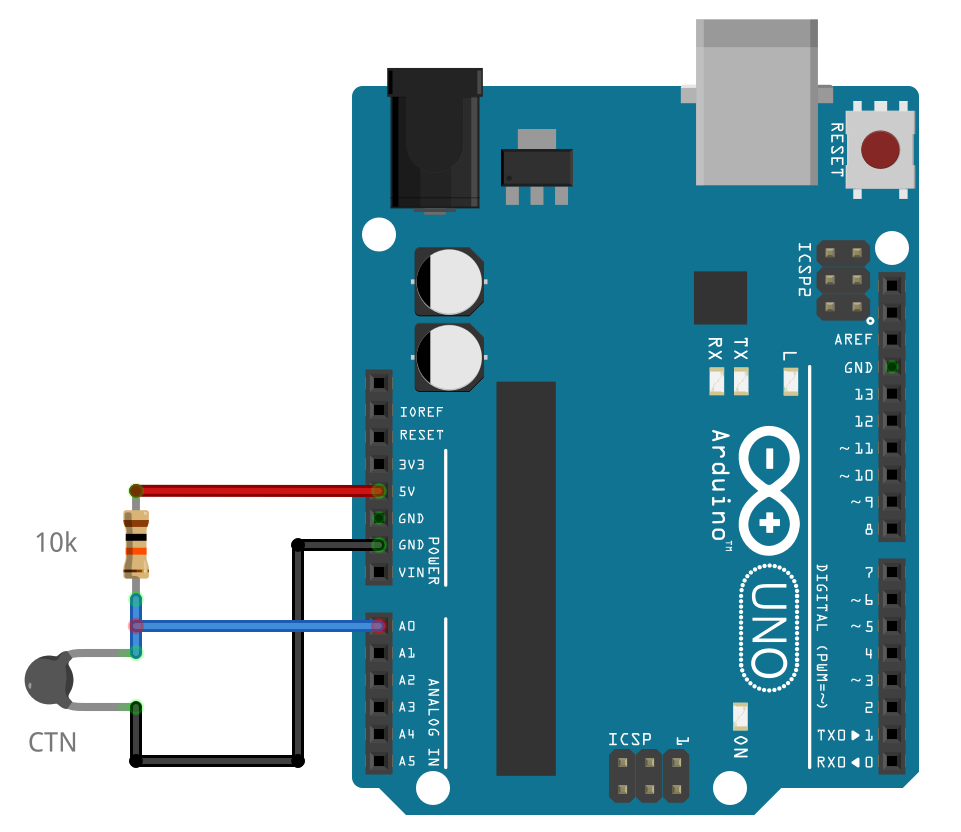
Mesure de la résistance d’une CTN sur l’entrée analogique A0
/*
* Mesure de la résistance d'une CTN
*/
// Déclaration des variables pour la mesure de la résistance
float Vcc = 5.0; // Tension d'alimentation
float R1 = 10000; // Résistance du pont diviseur de tension
float U; // Tension de la CTN en volt
float R_mes; // Résistance mesurée de le CTN en Ohm
void setup() {
Serial.begin(9600); // Paramétrage du port série
}
void loop() {
U = analogRead(A0)*Vcc/1023; // Lecture tension en V
R_mes = R1*U/(Vcc-U); // Calcul de la résistance
Serial.print("R = "); // Affichage
Serial.print(R_mes); // Affichage
Serial.println(" Ohm"); // Affichage + sout de ligne
delay(1000); // Temporisation de 1s
}
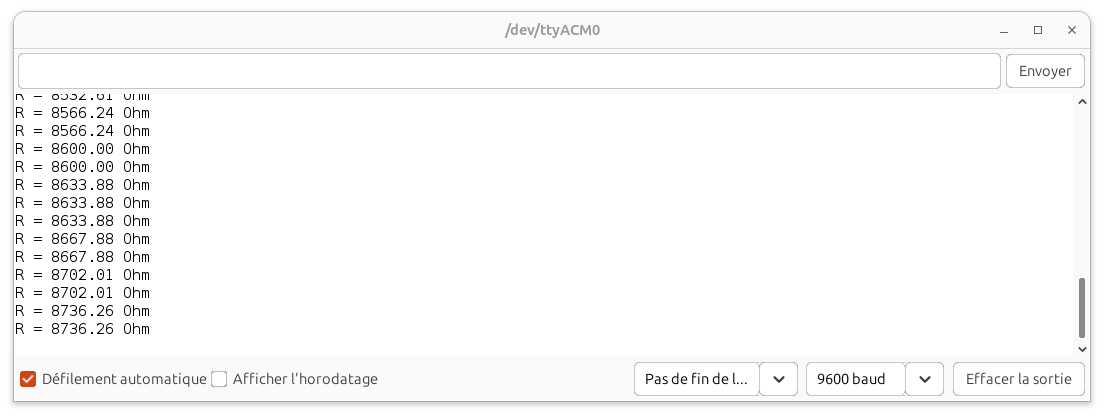
Résultats dans le moniteur série d’Arduino IDE
Programme 2 : thermomètre numérique (application)

Mesure de la température donnée par une CTN sur l’entrée analogique A0
Rappel de relation simplifiée de Steinhart-Hart :
avec pour notre CTN :
/*
* Mesure de la résistance d'une CTN et
* Calcul de la température à partir de la relation simplifiée de Steinhart-Hart
*/
// Déclaration des variables pour la mesure de la résistance
float Vcc = 5.0; // Tension d'alimentation
float R1 = 10000; // Résistance du pont diviseur de tension
float U; // Tension CTN en volt
float R_mes; // Résistance CTN en ohm
// Déclaration des variables pour la calcul de la température
float T0 = 25; // Température de référence (25°C)
float R0 = 10600; // Resistance R0 à T0 = 25°C
float beta = 3440; // Coefficient de temperature en K
float inverse; // Inverse de la temperature en K-1
float T_K; // Temperature en K
float T; // Temperature en °C
void setup() {
Serial.begin(9600); // Paramétrage du port série
}
void loop() {
U = analogRead(A0)*5.0/1023; // Lecture de la tension en V
R_mes = R1*U/(Vcc-U); // Calcul de la résistance mesurée
Serial.print("R = "); // Affichage
Serial.print(R_mes); // Affichage
Serial.println("Ohm"); // Affichage + retour à la ligne
inverse = 1/beta * log(R_mes/R0) + 1/(T0+273.15); // Calcul de l'inverse de la temperature
T_K = 1/inverse; // Calcul de la température en Kelvin
T = T_K - 273.15; // Caclul de la température en °C
Serial.print("T = "); // Affichage
Serial.print(T); // Affichage
Serial.println("°C"); // Affichage + retour à la ligne
delay(1000); // Pause
}
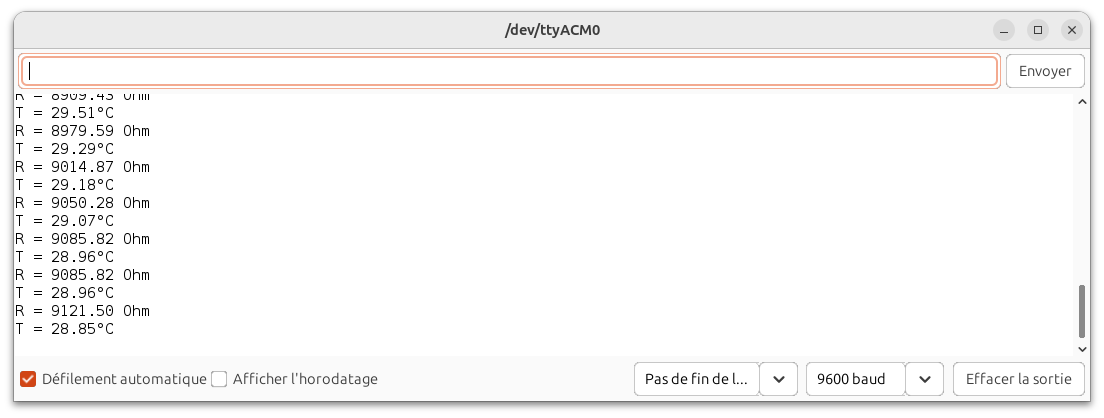
Résultats dans le moniteur série d’Arduino IDE
A retenir
Placer un capteur résistif (température, pression, lumière, …) dans un pont diviseur de tension reste une solution simple pour mesurer sa résistance à l’aide d’un microcontrôleur.