Cas d’un capteur résistif CTN
Principe
Une CTN est un capteur résistif à coefficient de température négatif.
Le but est de réaliser un étalonnage du capteur et d’en déduire un modèle. A partir de ce modèle, un programme Arduino pourra calculer et afficher la température donnée par ce capteur..
Courbe d’étalonnage
Les mesures sont effectuées avec un thermomètre et un ohmmètre.
T (°C) |
R (\(\Omega\)) |
|---|---|
2.4 |
25455 |
5.1 |
22714 |
10.0 |
18622 |
15.1 |
15201 |
20.0 |
12607 |
25.0 |
10475 |
30.0 |
8740 |
35.1 |
7333 |
40.0 |
6194 |
45.0 |
5217 |
50.0 |
4358 |
55.1 |
3689 |
60.0 |
3120 |
65.1 |
2647 |
70.1 |
2264 |
75.1 |
1926 |
80.0 |
1658 |
Téléchargement : data_ctn_1.txt (mesures au format CSV).
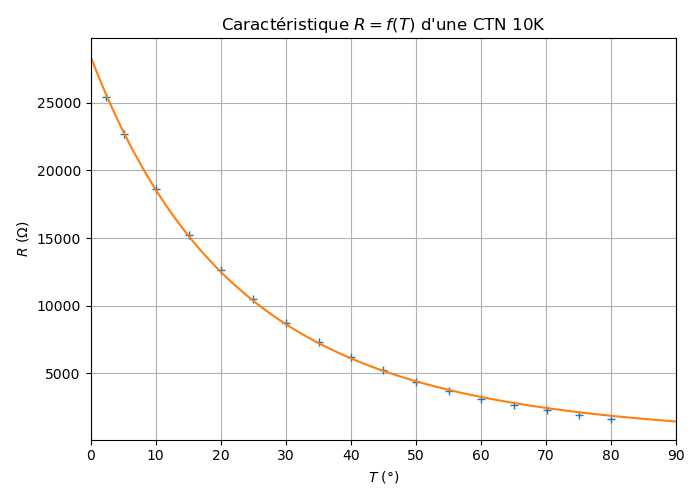
Courbe d’étalonnage d’une CTN 10k
Note
Dans cette CTN, la résistance mesurée prend la valeur particulière de 10 \({\rm k\Omega}\) pour 25°C !
Relation de Steinhart-Hart
Sur une grande plage de variation, la relation entre la température (en K) et la résistance de la CTN est :
A, B et C sont les coefficients de Steinhart-Hart. Ils sont donnés par le constructeur
ou peuvent se déterminer expérimentalement à l’aide du programme Python steinhart-hart.py à partir de trois points de la courbe d’étalonnage.
Résultats obtenus à partir du programme Python :
Relation simplifiée de Steinhart-Hart
Sur une plage de variation plus réduite de la température, la relation de Steinhart-Hart permet d’écrire :
\({R_0}\) est la valeur de la résistance pour la température \({T_0}\).
\({\beta}\) est le coefficient de température (en K).
Ces coefficients sont généralement donnés par le constructeur (datasheet).
Module |
Référence CTN |
\(R_0~{\rm (k\Omega)}\) |
\(\beta~{\rm (K)}\) |
|---|---|---|---|
Grove - Temperature Sensor V1.2 |
NCP18WF104F03RC |
\(100\) |
\(4255~(25/80{\rm^\circ C})\) |
Velleman VMA320 |
NTC-MF52 3950 |
\(10\) |
\(3950\) |
Note
Expression de la constante \(\beta\) à partir des températures \(T_0\) et \(T\) :
Les coefficients \({R_0}\) et \({\beta}\) peuvent être également déterminés par une modélisation de la caractéristique sur la plage de température d’utilisation de la CTN.
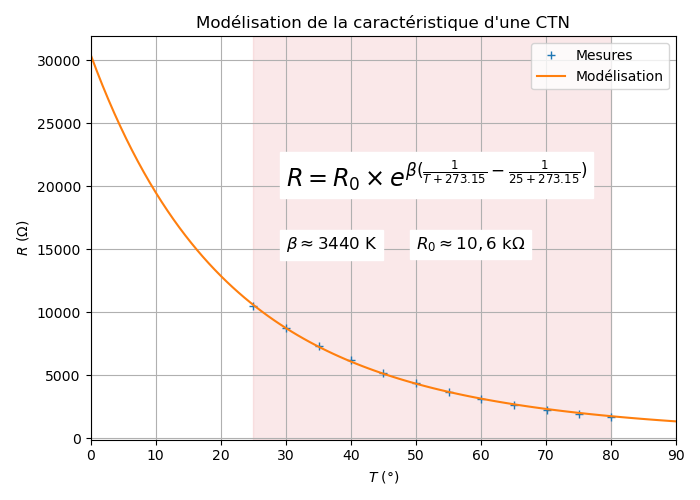
Modélisation de la caractéristique de la CTN de 25°C à 80°C
Résultat de la modélisation de \(T_0 = 25{\rm^\circ C}\) à \(80{\rm^\circ C}\) :
Inversement, le calcul de la température (en K) s’obtient à partir de la relation suivante :
Programme 1 : mesure de la résistance de la CTN
La CTN est connectée à la masse (montage 1). L’entrée analogique A0 mesure la tension du capteur.
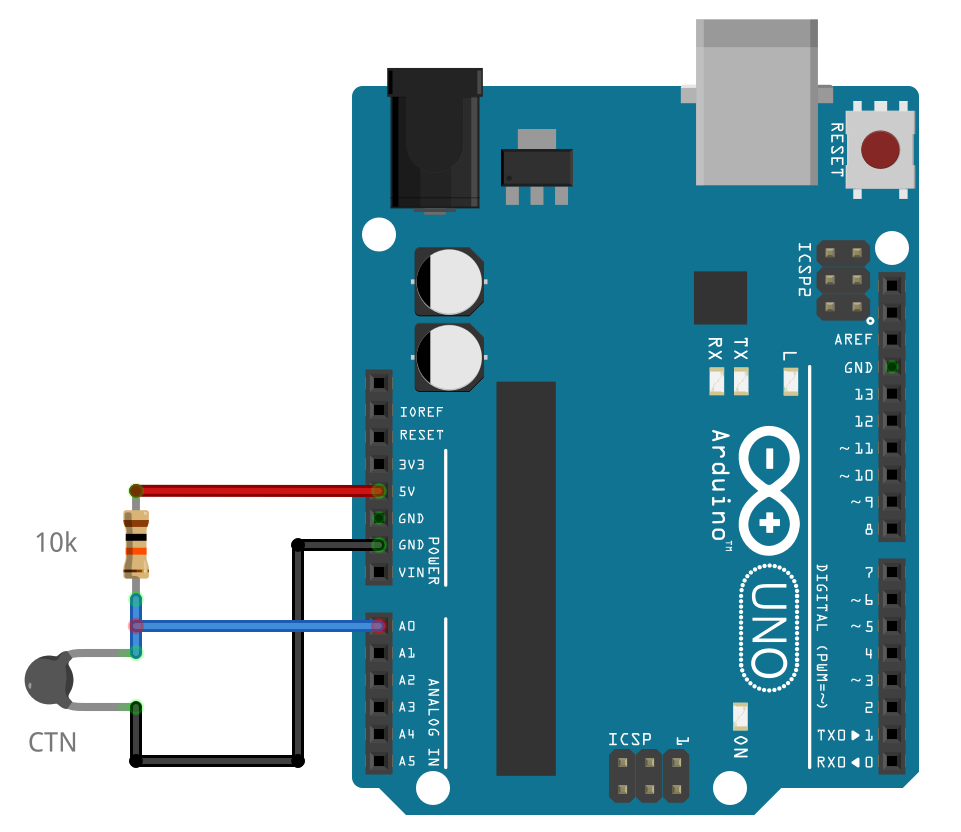
Mesure de la résistance d’une CTN sur l’entrée analogique A0
/*
* Mesure de la résistance d'une CTN
* David THERINCOURT - 2025
*/
float Vcc = 5.0; // Tension d'alimentation
float R1 = 10000; // Résistance du pont diviseur de tension
float U; // Tension de la CTN en volt
float R_mes; // Résistance mesurée de le CTN en Ohm
void setup() {
Serial.begin(9600); // Paramétrage du port série
}
void loop() {
U = analogRead(A0)*Vcc/1023; // Lecture tension en V
R_mes = R1*U/(Vcc-U); // Calcul de la résistance
Serial.print("R = "); // Affichage
Serial.print(R_mes,0); // ...
Serial.println(" Ohm"); // ...
delay(1000); // Temporisation de 1s
}
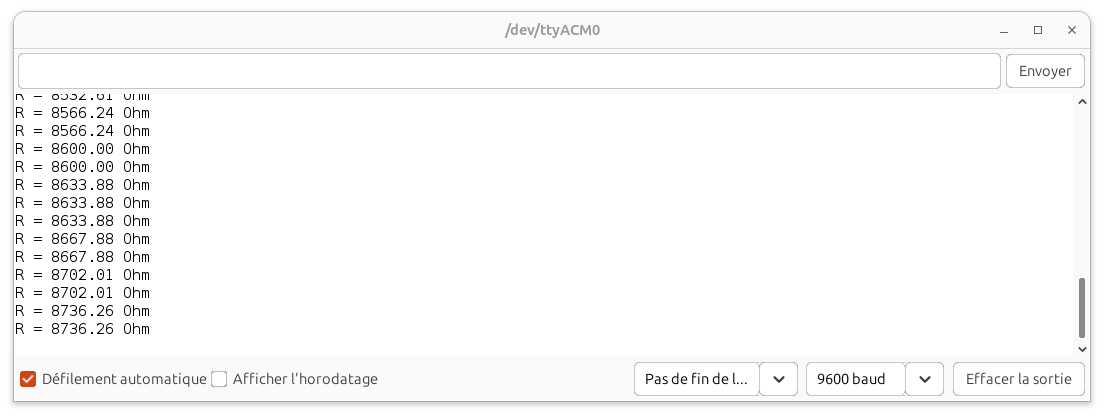
Résultats dans le moniteur série d’Arduino IDE
Programme 2 : thermomètre numérique (application)

Mesure de la température donnée par une CTN sur l’entrée analogique A0
Rappel de relation simplifiée de Steinhart-Hart :
avec pour notre CTN :
/*
* Mesure de la résistance d'une CTN et
* Calcul de la température à partir de la relation simplifiée de Steinhart-Hart
* David THERINCOURT - 2025
*/
float Vcc = 5.0; // Tension d'alimentation
float R1 = 10000; // Résistance du pont diviseur de tension
float U; // Tension CTN en volt
float R_mes; // Résistance CTN en Ohm
float T0 = 25 + 273.15; // Température de référence en K (T0 = 25°C)
float R0 = 10600; // Résistance R0 à T0 = 25°C
float beta = 3440; // Coefficient de température en K
float inverse; // Inverse de la température en K-1
float T_K; // Température en K
float T; // Température en °C
void setup() {
Serial.begin(9600); // Paramétrage du port série
}
void loop() {
U = analogRead(A0)*5.0/1023; // Lecture de la tension en V
R_mes = R1*U/(Vcc-U); // Calcul de la résistance mesurée
Serial.println("--------"); // Affichage
Serial.print("R = "); // ...
Serial.print(R_mes, 0); // ...
Serial.println(" Ohm"); // ...
inverse = 1/beta * log(R_mes/R0) + 1/T0; // Calcul inverse temperature en K^-1
T_K = 1/inverse; // Calcul température en K
T = T_K - 273.15; // Caclul température en °C
Serial.print("T = "); // Affichage
Serial.print(T); // ...
Serial.println(" °C"); // ...
delay(1000); // Temporisation
}
Résultats dans le moniteur série d’Arduino IDE