Mesurer une pression - Loi de Mariotte (première générale)
Principe
La manipulation consiste à vérifier la loi de Mariotte \({P \times V = constante}\) (à température et quantité de matière constantes).
Capteur de pression absolue MPX5700AP
Le MPX5700AP est un capteur analogique de pression absolue (15 kPa à 700 kPa - 5V).
Capteur MPX5700AP Grove (15 kPa à 700 kPa) (image : seeedstudio)
Schéma électrique (source : Freescale Semiconductor, Inc.)
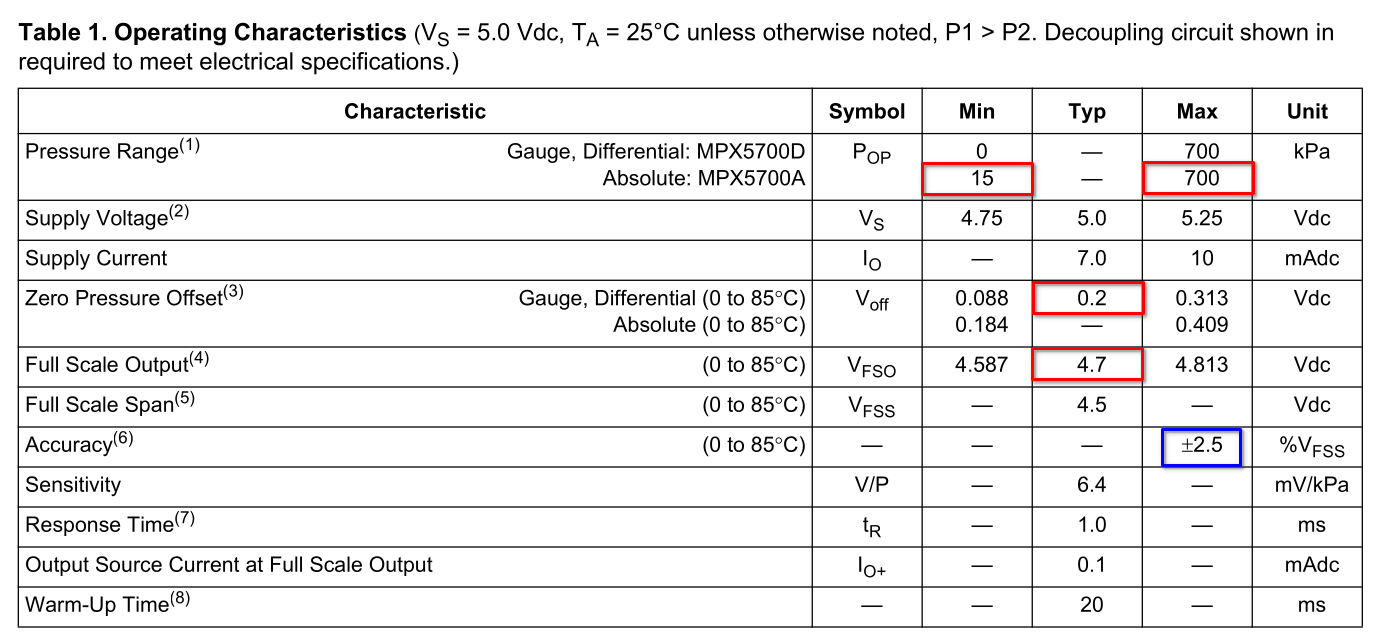
Caractéristiques (source : Freescale Semiconductor, Inc.)
La mesure de pression (en kPa) est donnée par la relation pour une alimentation de 5 V :
\[\boxed{P = \dfrac{P_{max}-P_{min}}{V_{max}-V_{min}} \times (v_{out}-V_{min}) + P_{min}}\]
Soit :
\[P = \dfrac{700-15}{4,7-0,2} \times (v_{out}-0,2) + 15 \quad\implies\quad P \approx 152\times (v_{out}-0,2) + 15\]
Capteur de pression absolu MPXHZ6400A (Educaduino LAB)
Le MPXHZ6400A est un capteur analogique de pression absolue (20 kPa à 400 kPa - 5V).

Capteur MPX6400A Educaduino LAB
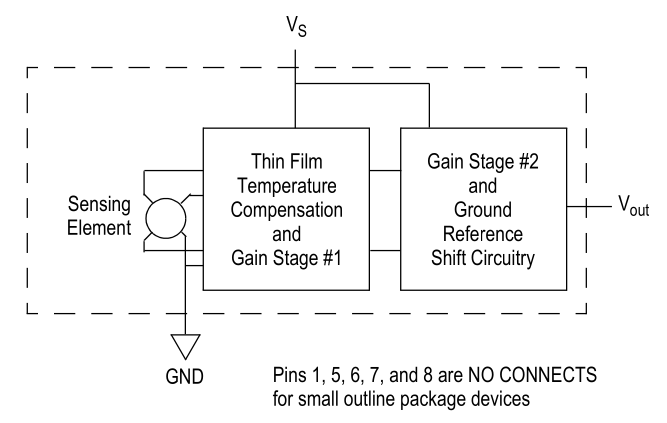
Schéma électrique (source : Freescale Semiconductor, Inc.)
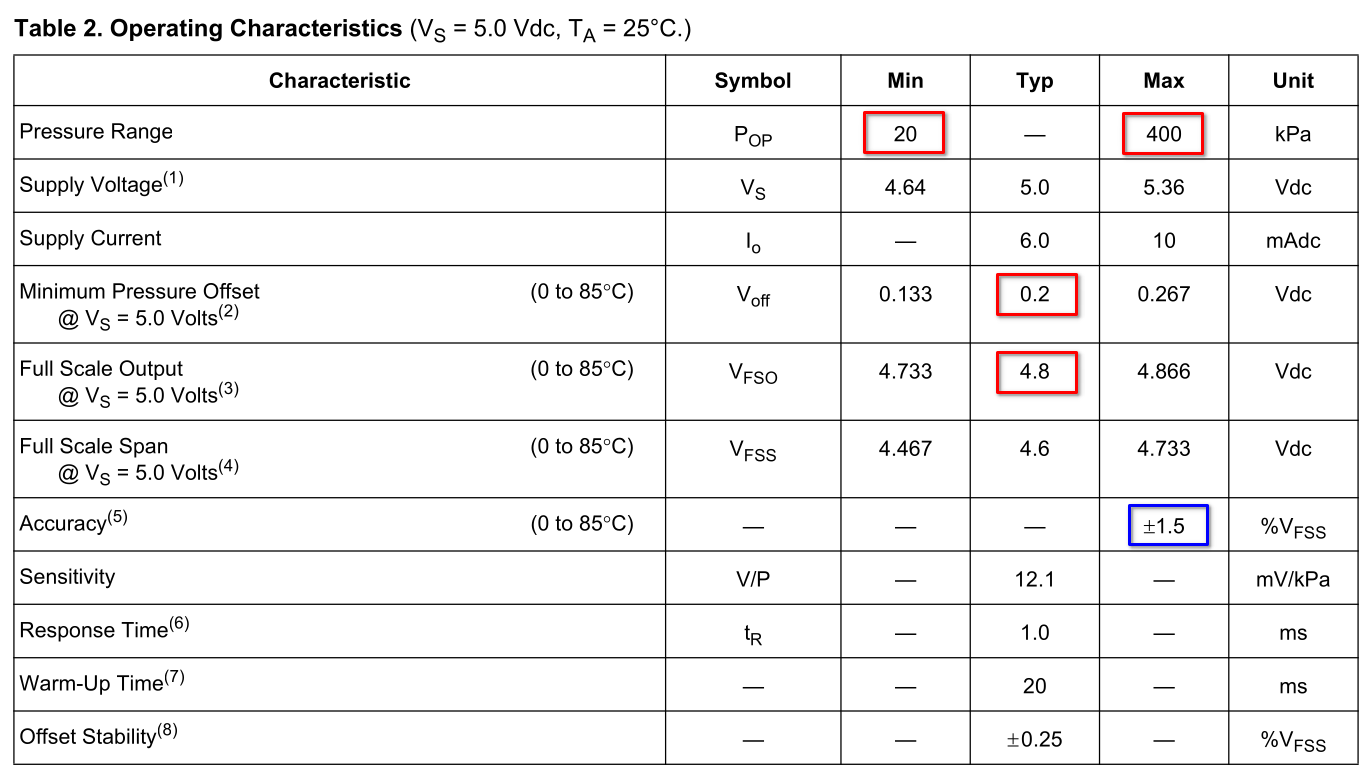
Caractéristiques (source : Freescale Semiconductor, Inc.)
La mesure de pression (en kPa) est donnée par la relation pour une alimentation de 5 V :
Soit :
\[P = \dfrac{400-20}{4,8-0,2} \times (v_{out}-0,2) + 20 \quad\implies\quad P \approx 82,6\times (v_{out}-0,2) + 20\]
Arduino (C/C++)
Le montage est composé d’une carte Educaduino Lab, d’un capteur de pression Educaduino (MPXHZ6400A / 20 kPa à 400 kPa) et d’une seringue.
Mesure d’une pression avec Educaduino Lab
Note
Dans cette manipulation, il est important de tenir compte du volume d’air \({V_0}\) présent dans le tube. La loi de Mariotte s’écrit alors
1/*
2 * Mesure d'une pression absolue
3 * Capteur Educaduino 20 kPa à 400 kPa
4 * branché sur la broche A9
5 */
6
7#define brocheCapteur A9 // Numéro de broche connectée au capteur
8#include <LiquidCrystal.h> // Librairie de gestion de l écran LCD
9
10LiquidCrystal lcd(12, 11, 5, 4, 3, 2); // Déclaration de l écran LCD
11
12
13float tension ; // Tension mesurée
14float pression ; // Pression mesurée
15
16void setup() {
17 lcd.begin(16, 2); // Paramétrage de l ecran LCD
18
19}
20
21void loop() {
22 tension = analogRead(brocheCapteur)*5.0/1023 ; // Lecture de la tension
23 pression = 82.6*(tension-0.2) + 20 ; // Calcul de la pression en kPa
24 lcd.clear(); // Début affichage
25 lcd.setCursor(0,0);
26 lcd.print("Pression en kPa");
27 lcd.setCursor(0,1);
28 lcd.print(pression); // Fin affichage
29 delay(1000);
30}
Résultats :
V (mL) |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
P (kPa) |
96,5 |
105 |
114 |
124 |
136 |
152 |
171 |
194 |
227 |
Arduino (Python/Nanpy)
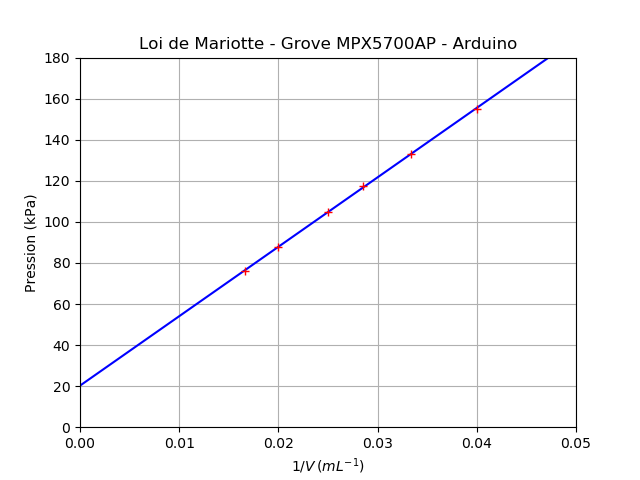
Cet exemple utilise un module Grove MPX5700AP (15-700 kPa). Les mesures sont affichées au format CSV pour exploitation avec un tableur, Regressi, Latis ou Python par un copier-coller.
# Vérification de la loi de Boyle-Mariotte avec module Grove MPX5700AP 15-700 kPa > 0.2-4.7 V
from nanpy import ArduinoApi # Gestion de la carte Arduino
from nanpy import SerialManager # Gestion du port série
port = SerialManager(device='/dev/ttyACM0') # Sélection du port série (exemple : device = 'COM6')
uno = ArduinoApi(connection=port) # Déclaration de la carte Arduino
Pmin = 15 # Pression minimale en kPa
Pmax = 700 # Pression maximale en kPa
Umin = 41 # Tension minimale 0.2/5*1023 = 41
Umax = 962 # Tension maximale 4.7/5*1023 = 962
volume = [60,50,40,35,30,25] # Proposition de volumes - 40 mL pour pression atmosphérique
pression = [] # Tableau des pressions
# Mesures
for vol in volume : # Parcours des volumes prédéfinis
input("Régler le volume sur " + str(vol) + " mL") # Validation du réglage du volume
U = uno.analogRead(0) # Lecture de la tension numérique (10 bit)
P = (Pmax-Pmin)/(Umax-Umin)*(U-Umin) + Pmin # Calcul de la pression
print(P, "kPa") # Affichage de la pression
pression.append(P) # Ajout de la mesure dans le tableau de pression
# Affichage au format CSV
print("V ; P") # Affichage entête des grandeurs
print("mL ; hPa") # Affichage entête des unités
for i in range(len(volume)): # Parcours des points de mesures
print(volume[i],";",pression[i]) # Affichage des mesures
Résultats :
Régler le volume sur 60 mL
75.98805646036917 kPa
Régler le volume sur 50 mL
87.88816503800217 kPa
Régler le volume sur 40 mL
104.99457111834963 kPa
Régler le volume sur 35 mL
117.63843648208469 kPa
Régler le volume sur 30 mL
133.25732899022802 kPa
Régler le volume sur 25 mL
154.82627578718783 kPa
V ; P
mL ; kPa
60 ; 75.98805646036917
50 ; 87.88816503800217
40 ; 104.99457111834963
35 ; 117.63843648208469
30 ; 133.25732899022802
25 ; 154.82627578718783
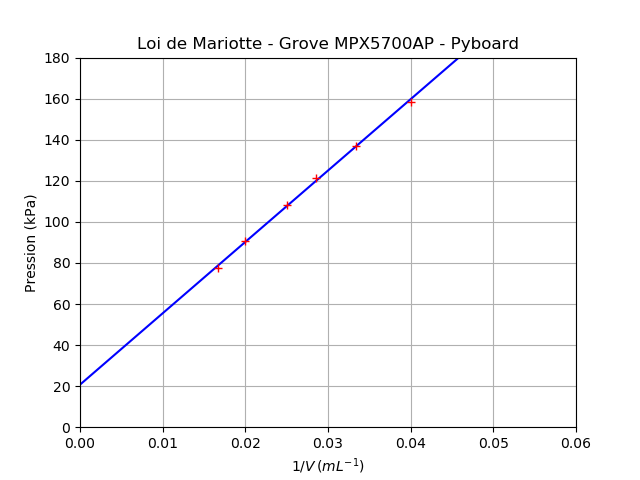
Pyboard (Micropython)
Cet exemple utilise également un module Grove MPX5700AP (15-700 kPa). Les mesures sont affichées au format CSV pour exploitation avec un tableur, Regressi, Latis ou Python par un copier-coller.
# Vérification de la loi de Boyle-Mariotte avec module Grove MPX5700AP 15-700 kPa > 0.2-4.7 V
from pyb import Pin, ADC
adc = ADC(Pin("A0")) # Déclaration du CAN
Pmin = 15 # Pression minimale
Pmax = 700 # Pression maximale
# Amplification = 3,3/4,7 = 0.702
Umin = 174 # Tension minimale (0.2V * 0.702 = 0.140V) N=174
Umax = 4095 # Tension maximale (4.7V * 0.702 = 3.300V) N=4095
volume = [60,50,40,35,30,25] # Proposition de volumes - 40 mL pour pression atmosphérique
pression = [] # Tableau des pressions
# Mesures
for vol in volume : # Parcours des volumes prédéfinis
input("Régler le volume sur " + str(vol) + " mL") # Validation du réglage du volume
U = adc.read() # Lecture de la tension numérique (12 bit)
P = (Pmax-Pmin)/(Umax-Umin)*(U-Umin) + Pmin # Calcul de la pression du capteur
print(P, "kPa") # Affichage de la pression
pression.append(P) # Ajout de la mesure dans le tableau de pression
# Affichage au format CSV
print("V ; P") # Affichage entête des grandeurs
print("mL ; hPa") # Affichage entête des unités
for i in range(len(volume)): # Parcours des points de mesures
print(volume[i],";",pression[i]) # Affichage des mesures
Résultats :
Régler le volume sur 60 mL
79.81383 kPa
Régler le volume sur 50 mL
91.69345 kPa
Régler le volume sur 40 mL
109.1635 kPa
Régler le volume sur 35 mL
122.0913 kPa
Régler le volume sur 30 mL
137.4649 kPa
Régler le volume sur 25 mL
157.7302 kPa
V ; P
mL ; kPa
60 ; 79.81383
50 ; 91.69345
40 ; 109.1635
35 ; 122.0913
30 ; 137.4649
25 ; 157.7302
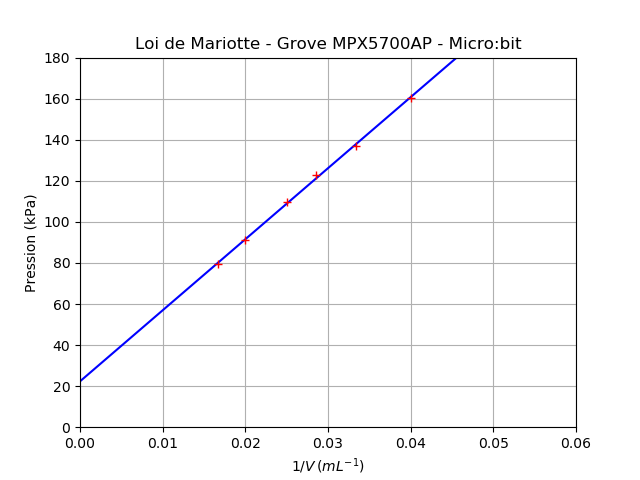
Micro:bit (Micropython)
Cet exemple utilise également un module Grove MPX5700AP (15-700 kPa). Les mesures sont affichées au format CSV pour exploitation avec un tableur, Regressi, Latis ou Python par un copier-coller.
# Vérification de la loi de Boyle-Mariotte avec module Grove MPX5700AP 15-700 kPa > 0.2-4.7 V
from microbit import *
Vcc = 3.09 # Mesure au voltmètre entre 3V3 et GND
No = 4 # Décalage (entier) obtenu pour une tension de OV
Pmin = 15 # Pression minimale
Pmax = 700 # Pression maximale
# Amplification = 3,3/4,7 = 0.702
Umin = 0.14 # Tension minimale (0.2V * 0.702 = 0.140V) N=44
Umax = 3.3 # Tension maximale (4.7V * 0.702 = 3.300V) N=1023
volume = [60,50,40,35,30,25] # Proposition de volumes - 40 mL pour pression atmosphérique
pression = [] # Tableau des pressions
# Mesures
for vol in volume : # Parcours des volumes prédéfinis
input("Régler le volume sur " + str(vol) + " mL") # Validation du réglage du volume
N = pin1.read_analog() # Lecture de la tension numérique (10 bit)
U = (N-No)*Vcc/(1023-No) # Calcul de la tension
P = (Pmax-Pmin)/(Umax-Umin)*(U-Umin) + Pmin # Calcul de la pression
print(P, "kPa") # Affichage de la pression
pression.append(P) # Ajout de la mesure dans le tableau de pression
# Affichage au format CSV
print("V ; P") # Affichage entête des grandeurs
print("mL ; hPa") # Affichage entête des unités
for i in range(len(volume)): # Parcours des points de mesures
print(volume[i],";",pression[i]) # Affichage des mesures
Résultats :
Régler le volume sur 60 mL
79.3083 kPa
Régler le volume sur 50 mL
91.1404 kPa
Régler le volume sur 40 mL
109.546 kPa
Régler le volume sur 35 mL
122.693 kPa
Régler le volume sur 30 mL
137.154 kPa
Régler le volume sur 25 mL
160.161 kPa
V ; P
mL ; kPa
60 ; 79.3083
50 ; 91.1404
40 ; 109.546
35 ; 122.693
30 ; 137.154
25 ; 160.161